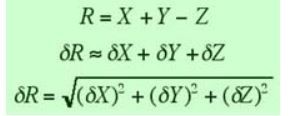Definition And Calculation Of Error Propagation In Statistics

Asked By Maxwell Polen 0 points N/A Posted on - 11/02/2017

I am an 8th std. Student and I encountered an error with some uncertainty, and I am having difficulty in calculating that. How to calculate the error propagation in the experiments or statistics problems?

• Status: Open
• Question Views: 162
• Answer Count: 1
• Vote Up 0 Vote Down

• Answer Accepted: No
• Question Category: Others
• Question Tags: calculation error

Answered By Darline B Daniel 30 points N/A #305654

Definition And Calculation Of Error Propagation In Statistics

Propagation of uncertainty or propagation of error happens due to the variations in the experimented values. When you perform certain experiments, then the values calculated inhibits some errors due to the faulty measurements or instruments having precision.
This error is very common while working so we have to take a common error value called as delta (Δ) so that we can calculate the error propagation.

There are various ways to calculate for different kinds of uncertainty propagation, and it would be difficult to explain each of them. But being an 8th std. Student, you must have encountered with a nominal error problem so we will go with the easier and simpler way to calculate.

If you have x, y, and z as the proper values calculated and there are Δx, Δy, Δz as the uncertainty error values calculated through the précised instrument, then

R = X + Y – Z
ΔR = ΔX + ΔY + ΔZ
〖∆R〗^2= 〖∆X〗^2+ 〖∆Y〗^2+ 〖∆Z〗^2

This would be the proper and simpler calculation for the error propagation in any experiment or project.

About Darline B Daniel

Questions
25

Answers
60

Best Answers
16

• Vote Up 0 Vote Down

• Posted on - 11/02/2017
• Question Category: Others