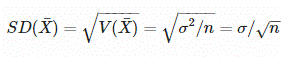Where Does √N Come From In Standard Error Of The Mean Formula?

In what way, does dividing by √N make sense in standard error mean formula, while calculating the z scores for multiple samples, and while describing the standard deviation of those means which is given as, Z=((x-μ))/□(σ/√N), where N is our sample size.